Общие сведения и основные понятия
Для оценки точности и эффективности диагностирования используется ряд показателей, основными из которых являются однозначность, чувствительность, стабильность и информативность. Проведем оценку с точки зрения предъявляемых к диагностическим параметрам требований.
Требование однозначности характеризуется отсутствием экстремума в зависимости диагностического параметра от структурного:
где dS, dx — изменение соответственно диагностического и структурного параметра.
Собранные статистические данные по износу деталей и диагностическим параметрам элементов автомобиля позволяют определить параметры зависимости диагностических параметров от структурных на компьютере.
Чувствительность диагностического параметра оценивается коэффициентом чувствительности
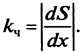
При линейной зависимости S от х (S=S0+bx) коэффициент чувствительности kч равен параметру b.
Стабильность диагностического параметра характеризуется величиной его рассеивания при неизменном значении структурного. Проведенные 25 независимых измерений диагностического параметра при неизменном значении структурного позволяют определить параметры распределения и абсолютную погрешность ΔS выбранного диагностического параметра tP,n по формуле
где tP,n — критерий Стьюдента при доверительной вероятности Р и числе измерений n; σS — среднеквадратическое отклонение единичного измерения параметра S. Относительная погрешность (точность) определяется делением абсолютной погрешности на среднее значение параметра.
Информативность диагностического параметра оценивается повышением вероятности состояния объекта диагностирования после диагностирования. Ее можно оценить по результатам анализа распределений диагностического параметра по исправным и неисправным объектам диагностирования. Такие распределения получают по результатам измерений указанных диагностических параметров по исправным и неисправным элементам. Для оценки значимости различия средних значений исправных S1 и неисправных S2 элементов, следовательно, информативности параметра S, определяют критерий Стьюдента

где σ — среднее значение среднеквадратических отклонений измеренных параметров у исправных и неисправных элементов; n1, n2 — объем выборок.
Если расчетный критерий Стьюдента tр больше критического /кр при доверительной вероятности 0,9, то различие S1 и S2 значимо с доверительной вероятностью 0,9 и выше, т. е. диагностический параметр можно считать информативным.
Об эффективности диагностирования можно судить по отношению удельных затрат при предупредительном ремонте с диагностированием С{ к удельным затратам при предупредительном ремонте без диагностирования при назначенной наработке С'2:
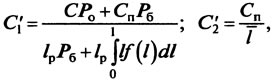
где С — стоимость устранения отказа; Ро — вероятность отказа; Рб — вероятность безотказной работы; lp — периодичность ремонта; f(l) — плотность распределения ресурса; Сп — стоимость предупредительного ремонта; l — средняя наработка на отказ.
Анализ затрат на устранение отказов и на их предупреждение показывает их отношение (коэффициент опасности отказа ко) и коэффициент вариации ресурса VR (выражение (1.4)). При этом сравнительная эффективность диагностирования определяется по результатам анализа их сочетания (рис. 1.16), т.е. проведение диагностирования позволяет в несколько раз сократить затраты по сравнению с ремонтом при назначенной наработке.
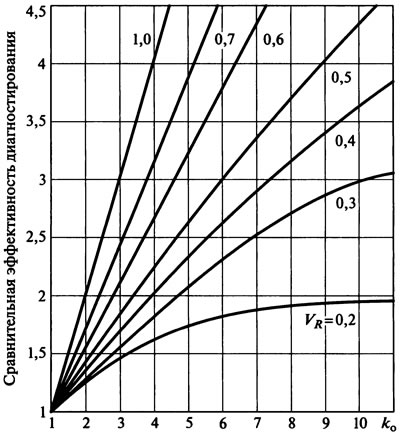
Рис. 1.16. Зависимость сравнительной эффективности диагностирования от вариации долговечности объекта VR и коэффициента опасности отказа ko
В качестве номинальных значений диагностических параметров целесообразно принять значения, которые должны быть при сборке агрегатов.
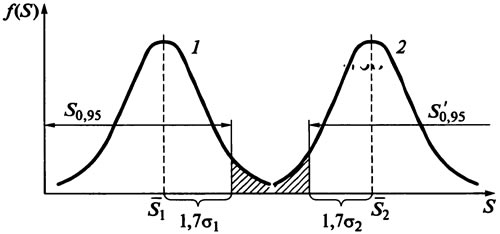
Рис. 1.17. Определение нормативного значения диагностического параметра S по закону распределения исправных (1) и неисправных (2) объектов диагностирования (при возрастании S в процессе эксплуатации)
Предельное значение диагностического параметра определяется статистическим методом, затем его можно уточнить по экономическому критерию. По полученному распределению диагностических параметров исправных элементов определяются его основные параметры, по которым находятся предельные значения при одностороннем ограничении и доверительной вероятности Р≥0,95 (рис. 1.17):
где S1, σ1 — соответственно среднее значение и среднеквадратическое отклонение значения диагностического параметра исправных агрегатов.
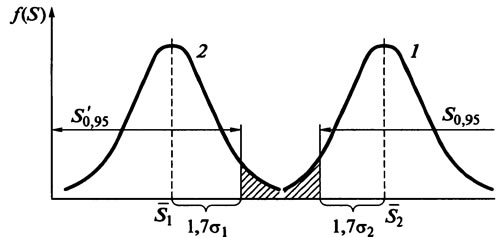
Рис. 1.18. Определение нормативного значения диагностического параметра S по закону распределения исправных (1) и неисправных (2) объектов диагностирования (при убывании S в процессе эксплуатации)
Для убывающих диагностических параметров определяется по формуле (рис. 1.18)
Предельную величину диагностического параметра можно определить путем измерения его у неисправных элементов. По ним надо также получить распределение и определить его параметры. В данном случае необходимо ограничение предельного значения диагностического параметра по нижнему пределу с вероятностью Р≥0,95; для убывающих диагностических параметров ограничение берется по верхнему пределу:
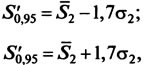
где S2, σ2 — соответственно среднее значение и среднеквадратическое отклонение диагностического параметра неисправных элементов.
При различиях в предельных значениях, определенных по группе исправных и неисправных элементов, поскольку их неисправности не всегда обусловлены техническим состоянием (изношенностью) деталей, в качестве предельных целесообразно принимать значения, полученные по исправным элементам. В дальнейшем нормативы следует уточнить по экономическому критерию.
Проведенный анализ надежности элементов позволяет определить периодичность диагностирования по экономико-вероятностному методу, в соответствии с которым определяется по номограмме коэффициент оптимальной периодичности μопт и в зависимости от коэффициента опасности отказа и коэффициента вариации ресурса:
где Lд — периодичность диагностирования; R — средний ресурс элемента.
При определенном коэффициенте опасности отказов ко и коэффициенте вариации Их коэффициент оптимальной периодичности цопт определяется по номограмме (рис. 1.19). При этом определяется периодичность диагностирования по формуле (1.21).
При принятой периодичности диагностирования допустимое (упреждающее) значение диагностического параметра VR определяется из зависимости диагностического параметра от наработки:
где i — число диагностирований с начала работы узла, при которых значение параметра изменилось от SН до Si; Sп, Sн — соответственно предельное и номинальное значение диагностического параметра.
С учетом зависимости диагностического параметра от наработки (по заданию) и расчета по формуле (1.22) определяют Sд.
Порядок выполнения работы
Техническое обеспечение и место выполнения — компьютерный класс, программные средства STATISTICA и Excel, набор карточек с данными для расчета статистических характеристик диагностического параметра.
Занятие проводится под руководством преподавателя с группой студентов.
После изучения методических указаний каждый студент получает персональные данные для расчета (экспериментальные значения диагностического параметра в зависимости от структурного, вариационные ряды диагностического параметра по исправным и неисправным агрегатам) и под контролем преподавателя выполняет необходимые вычисления по определению точности и нормативов диагностирования, используя при этом пример задания.
По окончании учебных занятий оформляется отчет по работе и осуществляется его защита.
Продолжительность работы — 2...4 ч.
Задание. Определить показатели точности и эффективности диагностирования
Дать оценку точности, нормативов и эффективности диагностирования технического состояния редуктора ведущего моста автомобиля КАМАЗ-5320 по исходным данным. Зависимость диагностического параметра (радиального зазора фланца ведущего вала) от структурного (износа шлицов ведущего вала), полученная путем сбора статистических данных, приведена в табл. 1.8.
Таблица 1.8. Зависимость радиального зазора фланца ведущего вала от износа шлицов ведущего вала редуктора
| Структурный параметр | 20 | 80 | 120 | 170 | 220 | 340 | 385 |
| Диагностический параметр | 20 | 100 | 120 | 160 | 290 | 560 | 630 |
Результаты 25 независимых измерений диагностического параметра при неизменном значении структурного представлены в табл. 1.9.
Для расчета точности принять доверительную вероятность Р=0,9.
Таблица 1.9. Вариационный ряд диагностического параметра
| Номер измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Значение параметра, мкм | 220 | 225 | 210 | 220 | 225 | 215 | 220 | 220 | 215 | 210 | 225 | 205 | 210 |
| Номер измерения | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Значение параметра, мкм | 220 | 215 | 220 | 215 | 220 | 210 | 205 | 210 | 220 | 215 | 220 | 210 |
Результаты измерения диагностического параметра 25 исправных и 25 неисправных редукторов ведущих мостов приведены в табл. 1.10.
Таблица 1.10. Вариационный ряд диагностического параметра S для исправных (S1) и неисправных (S2) редукторов
| Номер измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| S1, мкм | 150 | 160 | 155 | 150 | 165 | 150 | 140 | 145 | 150 |
| S2, мкм | 300 | 290 | 310 | 320 | 310 | 320 | 280 | 270 | 310 |
| Номер измерения | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| S1,мкм | 130 | 180 | 145 | 150 | 135 | 165 | 200 | 190 | 180 |
| S2, мкм | 250 | 320 | 260 | 280 | 335 | 300 | 325 | 290 | 330 |
| Номер измерения | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| S1,мкм | 140 | 170 | 155 | 160 | 140 | 120 | 130 |
| S2, мкм | 310 | 350 | 310 | 300 | 290 | 300 | 320 |
Пример 1.8. Пользуясь программой Excel, определяют параметры зависимости S от х (рис. 1.20):
где S0 — свободный член; b — коэффициент пропорциональности.
Из рис. 1.20 и формулы (1.23) видно, что требование однозначности выполняется, а коэффициент чувствительности kч=b=1,757, т. е. на каждую единицу изменения х величина S изменяется в 1,757 раза больше, что говорит о хорошей чувствительности диагностического параметра.
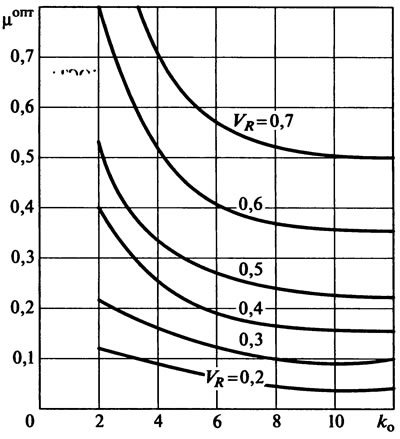
Рис. 1.20. Зависимость диагностического параметра S (радиального зазора фланца ведущего вала) от структурного параметра х (износа шлицов ведущего вала)
Пользуясь программным средством STATISTICA, по вариационному ряду (табл. 1.9) определяют параметры распределения (рис. 1.21): среднее значение S=216 мкм, среднеквадратическое отклонение σS=5,95 мкм. По формуле (1.19) находят абсолютную погрешность ΔS=2,02 мкм. Относительная погрешность с учетом среднего значения составит 0,93%.
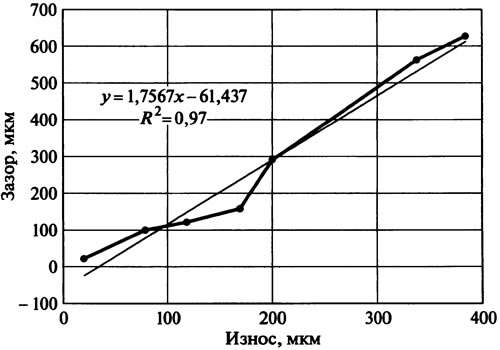
Рис. 1.21. Распределение диагностического параметра S при неизменном значении структурного х
Для оценки информативности, пользуясь программным средством STATISTICA, вычисляют параметры распределения диагностических показателей по исправным и неисправным редукторам (рис. 1.22). При этом используют вариационные ряды, представленные в табл. 1.9.
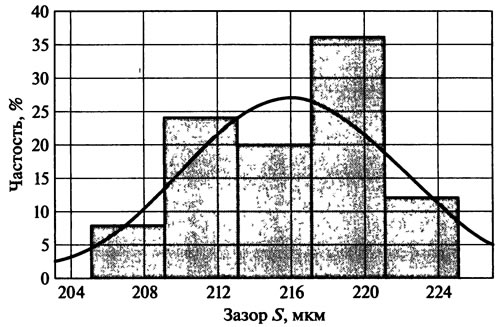
Рис. 1.22. Распределение диагностического параметра S по исправным (а) и неисправным (б) редукторам
Тогда среднее значение диагностического параметра по исправным объектам составит S1=154,2 мкм, по неисправным — S2=303,2 мкм, среднеквадратическое отклонение соответственно σ1=19,18 мкм, σ2=23,44 мкм.
По формуле (1.20) определяют расчетный критерий Стьюдента tр=25. Критическое значение критерия Стьюдента при n=25 и доверительной вероятности 0,95 составляет tкр=2,1, т.е. различие S1 и S2 значимо, а диагностический параметр информативен.
Содержание отчета
Отчет по работе должен отражать наиболее важные положения по методике оценки параметров точности, эффективности диагностирования и определения диагностических нормативов и включать в себя следующие сведения:
- название и цель работы;
- описание методики оценки параметров точности, эффективности диагностирования и определения диагностических нормативов;
- исходные данные и результаты расчетов параметров диагностирования элементов автомобиля;
- выводы по работе.
Контрольные вопросы
1. Перечислите основные требования к диагностическим параметрам.
2. Назовите диагностические нормативы и приведите формулы для их определения.
3. Каким параметром оценивается эффективность диагностирования?
